 IN A NUTSHELL: Regardless of the subject or the metric, you are either getting better or getting worse, you can’t be just “holding your own.” |
“Time Changes Everything.” “Everything Changes Over Time.” Said differently, or more technically, most things which you can measure can be considered as a function of time. This applies to most personal metrics:
- Your weight,
- Your career progression,
- Your achievement of key goals,
- Your net worth,
as well as to most business metrics:
- Your company’s revenue run rate,
- Your company’s profit run rate,
- The yield of a manufacturing process,
- The quality of your company’s products or services, or
- Your customer’s satsifaction with your offerings.
As a leader, when you ask people in your company how well you are doing on a certain key metric, they rarely tell you that things are rapidly getting worse. I’ve found that they also tend to under represent areas where you are doing well. I’ve found that the most common answers you are likely to hear are mediocre answers such as “it’s stable”, “it’s doing OK”, “so-so” or “we’re holding our own.”
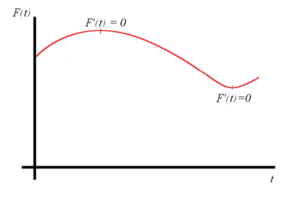
Well, if these answers are similar to the answers you usually get, I have a news flash for you. Your people are LYING to you! Here’s why. To get slightly technical again and take you back to Calc I, the slope of any function F(t) is defined by its first deriviative, F'(t). The only points where the function is not either increasing or decreasing are the local maxima or local minima, the points where F'(t) is equal to zero. Everywhere else, the function is either increasing or decreasing. Do the math!!
So other than for the occasional brief millisecond, your business has to either be constantly getting better or worse. If your people can’t tell you with conviction that things are getting better, chances are they are probably getting worse and you need to get on it!! Challenge those First Derivative assertions!! Keep the velocity positive!!